We present the Large Airfoil Model (LAM), consisting of Airfoil Surface Pressure Information Repository of Experiments (ASPIRE) and A Deep Airfoil Prediction Tool (ADAPT). The model employs a Deep Kernel Learning architecture, combining deep learning for active space mapping and a probabilistic method (Gaussian Process Regression) for uncertainty characterization. The LAM is a component of an interactive aerodynamics tool currently under development which allows users to perform complex aerodynamic design tasks (forward and inverse problems, 3D air load predictions, etc.) without the need for in-depth technical knowledge.
Airfoil Surface Pressure Information Repository of Experiments
Airfoil Surface Pressure Information Repository of Experiments (ASPIRE) is an open-source database accessible to the wider aerospace community utilizing the vast, nearly century-old historical repository of experimental airfoil data. It was first released on 11/11/2024 in a paper by Lee et al. (Link to preprint)
The database was established through an extensive data mining operation for strictly experimental pressure distributions for a variety of airfoils. Each entry of ASPIRE consist of experimental \(C_p\) measurements for various airfoil geometries, angles of attack (\(\alpha\)), chord-based Reynolds numbers (\(Re\)), and Mach numbers (\(M\)). The complete list of fully digitized as well as those in progress can be found here.
Available Data
ASPIRE consists of 2289 unique pressure distributions from 68 airfoils from various airfoil families and applications. All profiles of the airfoils included in the database, compared against the commonly studied NACA 0012, is shown below. Airfoil profiles thicker than a NACA 0012 at the given chordwise location are colored in varying shades of red. Profiles thinner than the NACA 0012 are colored in shades of blue.
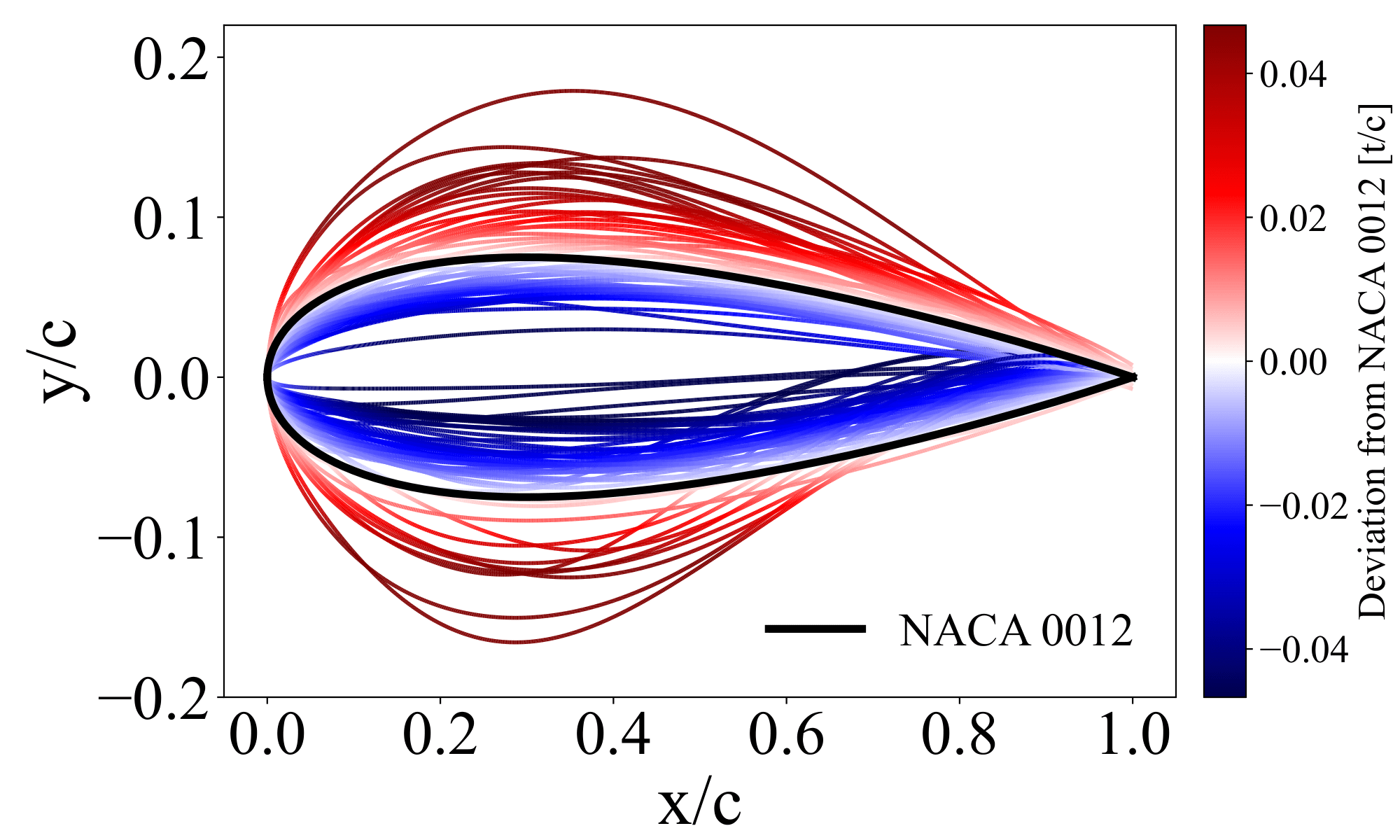
Geometric profiles of all airfoils in the database colored by their thickness compared to the baseline airfoil of NACA 0012
The available data ranges from \(-30^{\circ}\) to \(30^{\circ}\) in angles of attack (\(\alpha\)). The Mach number (\(M\)) of the data spans \(0.0\) to \(1.0\), from the incompressible regime to transonic and sonic regimes. The number of available pressure data in terms of unique airfoils at a given \(M\) and \(\alpha\) is shown in below. The color and the number in the center plot denotes the number of unique airfoils available for a given \(M\) - \(\alpha\) combination. Marginal histograms are plotted to provide a clear visualization of the available data at specific \(\alpha\) or \(M\). These are split in terms of airfoil families, design usage, and supercriticality.
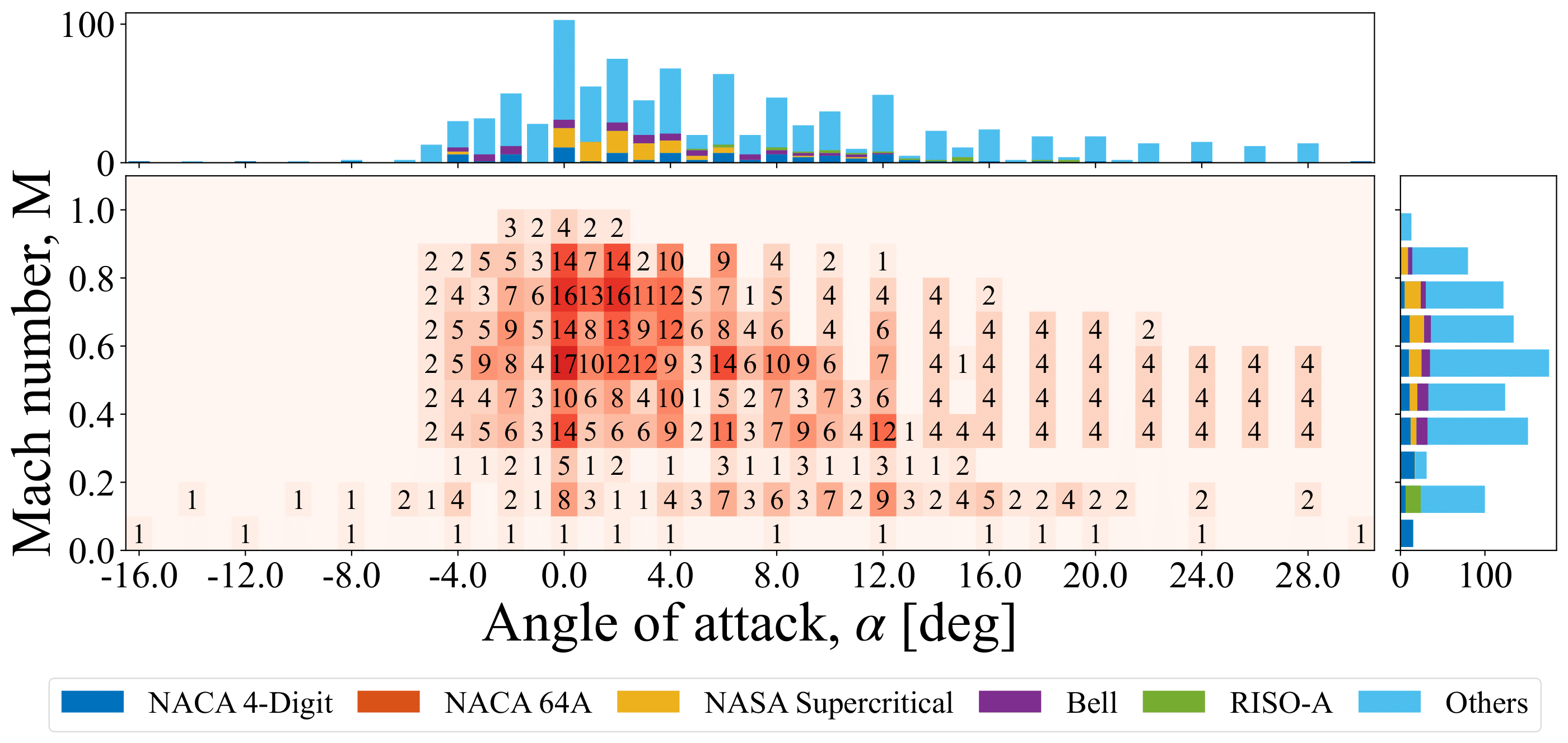
Distribution of available airfoil pressure data and the marginal histograms categorized by airfoil family

Distribution of available airfoil pressure data and the marginal histograms categorized by airfoil usage

Distribution of available airfoil pressure data and the marginal histograms categorized by supercritical airfoil
Last updated on 7/31/2024
Data Format
Each airfoil folder should contain 3 types of files: the coordinate file (csv), pressure data files (csv), and tag file (json).
Coordinates File
The coordinate files will define the geometry of the airfoil, with the first column being the normalized
chordwise location (\(x/c\)) and the second column being the normalized thickness (\(y/c\)) as seen below. The
order of the coordinates should start from the upper surface of the trailing edge (\(x/c = 1.0\)) to the leading
edge (\(x/c = 0.0\)) and end at the lower surface of the trailing edge (\(x/c = 1.0\)). The coordinate files
should be named: <airfoilname>_coordinates.csv.
Visualization of airfoil coordinates file format
Pressure File
Each CSV file consists of the airfoil pressure measurements along the entire wing chord at a given angle of
attack and Mach number. The file should follow the naming scheme of <airfoilname>_A<angle of attack> _M<Mach number>_Re<Reynolds number>_A.csv.
A negative angle of attack should have an “m” in front of the angle attack to denote the minus sign. For a
NACA0012 airfoil at \(\alpha = -2.1^\circ\), \(M = 0.3\), and \(Re = 3.0 \times 10^6\) would have the file name
NACA0012_Am2.1_M0.30_Re3e6_A.csv.
Just like the coordinates file, the first column corresponds to the normalized chordwise location (\(x/c\)) in the same order of Upper TE → LE → Lower TE. The second column is the pressure coefficient at the given chordwise location. The very first entry denotes the Mach number of the experiment. This format is visualized below.
Visualization of airfoil pressures file format
Tag File
In many sources, the experimental accuracy are reported by the authors within an report. These are often reported as a single scalar value in terms of the maximum magnitude of the error, or the maximum percentage error. These values were recorded in the ASPIRE in an accompanying tag file. Additionally, if the uncertainties in the independent variables such as those of the freestream Mach number, angles of attack, or pressure sensor locations were found in references, they were also reported in the tag files. An example of the tag file included in the database can be seen in below.

Format of tag files found for each experiment in ASPIRE
Getting Started
To access all airfoil experimental data in ASPIRE, run the following:
git clone https://github.com/hwlee924/Large-Airfoil-Model.git
cd Large-Airfoil-Model
A Deep Airfoil Prediction Tool
A Deep Airfoil Prediction Tool (ADAPT) is the deep probabilistic element of the Large Airfoil Model. Unlike existing ML models that are often trained on numerical simulations, we train on the experimental data made available from ASPIRE. We take advantage of the fact many experimental reports quantify and report measurement uncertainties. By taking a Bayesian approach in regression, the model can take into account experimental uncertainties during the training process and output the confidence intervals of the model predictions.
Specifically, ADAPT employs a Deep Kernel Learning architecture, combining deep learning for active space mapping and a probabilistic method for uncertainty characterization. For the deep learning component, a Fully Connected Neural Network (FCNN) [d-1000-1000-500-50-10] architecture is used. A Gaussian process (GP) model is applied to the final hidden layer of a neural network, conditioned on the output observations of \(C_p\). This approach allows us to construct kernels that capture the expressive power of deep neural network architectures. At its core, ADAPT is a Bayesian method, resulting in a multivariate Gaussian distribution over the space of \(C_p\) values. The choice of kernel for this GP model is the Matérn 5/2 kernel, which allows us to capture aerodynamic phenomena on airfoils such as rapid pressure changes at the suction peak, boundary layer transition from laminar to turbulent flow, and compressibility/shock effects. The overall structure of the model is shown in the figure below.
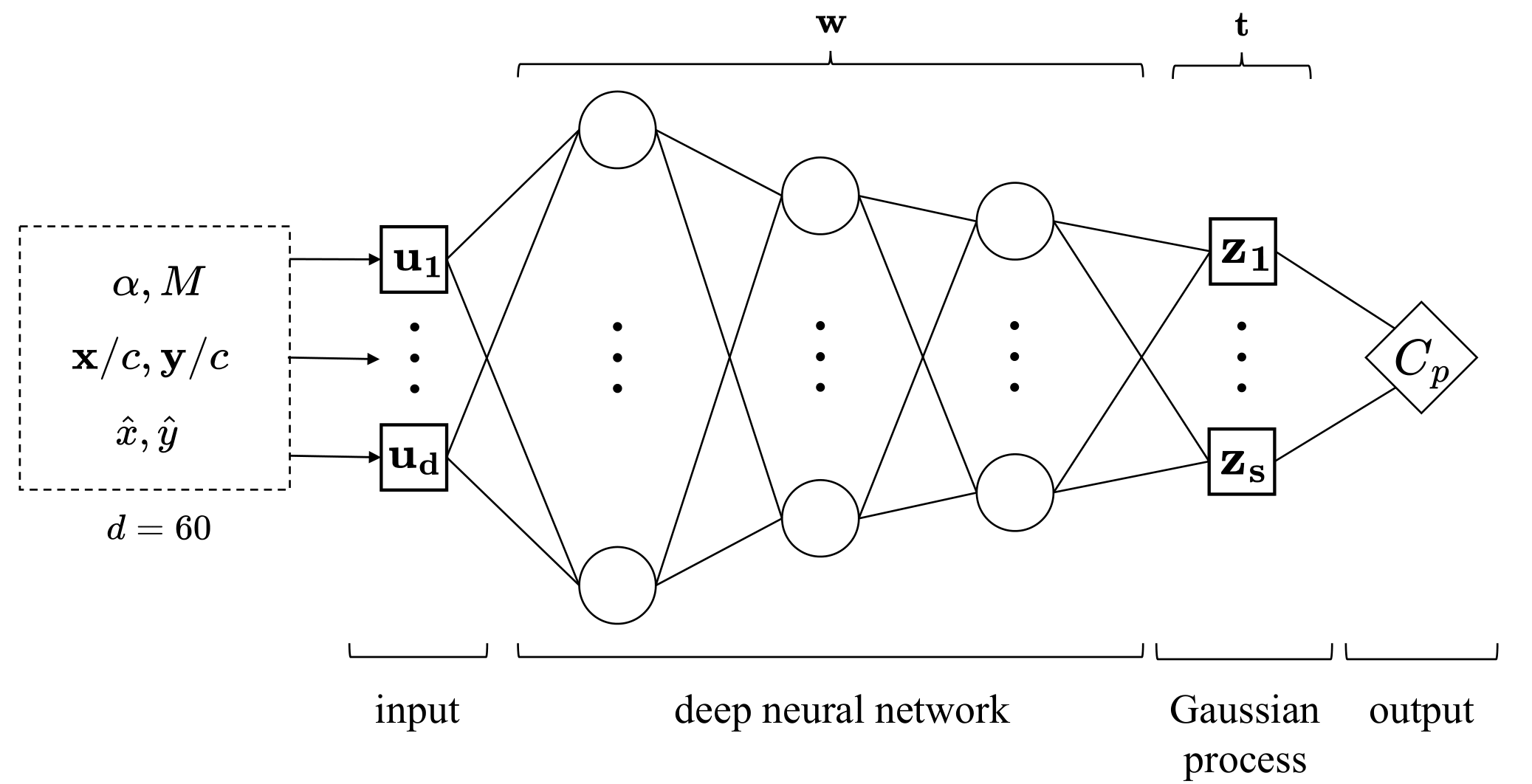
Overview of the Deep Kernel Learning model that maps a high dimensional training input containing airfoil geometry and flow conditions to predict \(C_p\) distribution